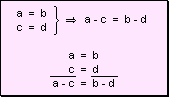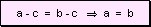matematicas

matematicas
andres

jueves, 26 de mayo de 2011

SUMA Y RESTA DE FRACCIONES


 SUMA Y RESTA DE FRACCIONES
Por: Dra. Luz M. Rivera y Melissa Murrias
Univerisidad Interamericana de Puerto Rico - Ponce
Reducción de Fracciones
Simplificación de Fracciones
Fracciones Mixtas e impropias
Suma de Fracciones
Resta de Fracciones
Multiplicación de Fracciones
División de Fracciones
Fórmulas para Recordar
Suma de Fracciones A
Objetivo:
  • Suma y resta de fracciones
  • Comparación de fracciones utilizando las reglas de proporción
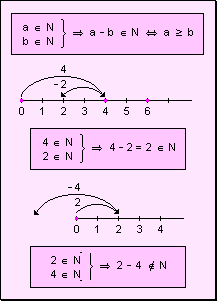
Utilizando un algoritmo sencillo podemos aprender a sumar fracciones mentalmente.
Veamos: Sean a /b   y c/d dos fracciones cualesquiera. Si las deseamos sumar podemos seguir la siguiente regla:
                    
      a   +   c   =       ad + bc     (se multiplica cruzado y los productos de suman)
      b        d                bd        (se multiplican los denominadores)
Veamos un ejemplo:
             El jefe de Cheo repartió los trabajos de contabilidad de urgencia entre algunos de los contables. A Cheo le tocó una cuarta parte (1/4) de los trabajos de urgencia más la tercera (1/3) parte del trabajo que le iba a tocar al empleado que faltó. En total , ¿que parte del trabajo tiene que realizar Cheo?


     
1   +  1    =    1(3) + 4(1)  = 3  + 4   =  7
4        3                (4)(3)           12          12
              

          
 Solución:   Cheo tuvo que realizar 7/12 del trabajo.

Notita para darle pensamiento: (para darle "coco")
¿A Cheo le tocó más de la mitad del trabajo o menos de la mitad del trabajo?
Solución:
Para comparar fracciones utilizamos las siguiente reglas de las proporciones
     a.   Si       a = c    entonces  ad = cb
                      b    d
     b.  Si          a < c    entonces  ad < cb
                      b    d
    c. Si         a > c    entonces  ad > cb
                    b    d

 
Volviendo a Cheo,   ¿7/12 es menor o mayor que 1/2 ?
             7   ?  1             7(2)  >   12(1), por lo  tanto     7   >  1
           12      2                                                            12      2
De modo que Cheo realizó más de la mitad del trabajo.
Veamos otro ejemplo:
A María le tocaba una tercera parte de la herencia de su padre. Su madre le cedió a ella dos quintas partes adicionales  que le tocaban a ella. ¿En total qué parte de la herencia la tocó a Maria?
Solución
1 + 2  = 1(5) + 3(2) = 5  + 6  = 11
3    5            15                15       15
A María le tocó  11/ 15 de la herencia de su padre.


Suma de Fracciones B
 
 Para sumar dos fracciones, hay  que tener en cuenta de que existen 2 tipos de fracciones:
 1. Fracciones homogéneas    (  1, 3, 5 )
                                                    4  4  4
 2. Fracciones heterogeneas  (  1, 2, 3 )
                                                    3  5  7
 Las fracciones homogéneas son las fracciones  que tienen el mismo  denominador; y las fracciones heterogeneas son las fracciones que tienen diferentes denominadores.
 
Ejemplo de suma de fracciones homogéneas:
   1 +  3  =  4  <Son fracciones homogéneas ya que
   5     5      5       tienen el mismo denominador. Las
                         fracciones  homogéneas, en suma, se
                        suman los numeradores y el
                        denominador se queda igual.>
 
2  + 3   = 5
7     7       7
Ejemplo de suma de fracciones heterogéneas:
 
 1 +1
 4   2                     <Aquí es diferente, las fracciones son
                               heterogéneas; los denominadores son
                                diferentes.>
 
Para sumar fracciones heterogéneas:
1. Se multiplican los denominadores.
2. Se multiplica cruzado y se coloca en el numerador.
3. Se suman los productos para obtener el numerador.
 
 
1  + 1
4     2

 Paso 1 :   1  + 1    =  ___           <Se multiplicaron los denominadores  4 · 2 = 8>
                   4     2          8
Paso 2 :  1  + 1   =  (2 ·1) + (4 · 1)   < Se multiplicó cruzado>
                  4     2                8
 
 
Paso 3:   2 + 4 =   6      < Se suman los productos para obtener el numerador.>
                    8          8
Paso 4:  6 ÷  2 =  3     < Se simplifica la fracción si es posible.>
                 8     2      4
 
 
 
 

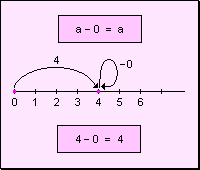
Resta de Fracciones
    En la resta de fracciones, se utilizan las mismas reglas de la suma de fracciones; pero en este caso hay que restar.
 
Ejemplo 1:
 
          5 - 1  = 4         Resta de Fracciones Homogéneas
          9    9     9
Ejemplo 2:
          2 - 1  =  ( 2 · 2) - (3 · 1)  = 4 - 3   = 1
           3   2                 6                    6        6 
Publicado por en No hay comentarios:

Ley de cierre

Ley de cierre
La sustracción de dos números naturales no es cerrada o completa ya que su resultado es un número natural si y sólo si el minuendo es mayor que el sustraendo.
Ley uniforme
La sustracción de dos números naturales es uniforme ya que su resultado es único. Si a ambos miembros de una igualdad se le resta un mismo número se obtiene otra igualdad.

Ley cancelativa
La ley cancelativa es la propiedad recíproca de la ley uniforme.
Elemento neutro
El número cero es el elemento neutro de la sustracción de números naturales.

Ley conmutativa
La sustracción de números naturales no es conmutativa, ya que depende del orden entre minuendo y sustraendo: al cambiar el orden de los mismos la diferencia varía.

Ley asociativa
La sustracción de números naturales no es asociativa, ya que depende de la forma que se asocien los operandos: si se reemplazan dos operandos por su diferencia efectuada, la diferencia final varía.
Publicado por en No hay comentarios:

Representación de números racionales en la recta numérica.

Representación de números racionales en la recta numérica.
Software para practicar
Recordemos que el conjunto de los números enteros se denota por $\input{Z.eepic}$ y se define de la manera siguiente:
\begin{displaymath}\input{Z.eepic}= \{ ..., -3, -2, -1, 0, 1, 2, 3, ... \}\end{displaymath}

Podemos representar los números enteros como puntos de una recta de la manera siguiente:
El segmento de recta comprendido entre dos números enteros consecutivos se llama "segmento unidad".
De manera similar, recordemos que el conjunto de los números racionales se denota por $\input{Q.eepic}$ y se define de la manera siguiente:
\begin{displaymath}\input{Q.eepic}=\left\{ \frac{a}{b} \;\; / \;\; a \in \input{Z.eepic}, b \in \input{Z.eepic}, b \not= 0 \right\}\end{displaymath}

Debido a que si $a \in \input{Z.eepic}$, $b \in \input{Z.eepic}$, $b > 0$ entonces se cumple que $\displaystyle \frac{a}{-b} = \frac{-a}{b}$; se conviene en representar los números racionales preferentemente por medio de fracciones en las cuales el denominador es un número entero positivo.
Recordemos además que si $a \in \input{Z.eepic}$, $b \in \input{Z.eepic}$, $b > 0$, el número racional $\displaystyle \frac{a}{b}$ se puede considerar como el cociente que se obtiene al dividir $a$ por $b$; en donde $b$ indica el número de partes en que se divide la unidad y $a$ el número de partes que se toman.
De esta manera, si se divide en dos partes iguales cada segmento unidad en la recta numérica, podemos representar los números racionales cuya representación fraccionaria tiene como denominador 2, como se muestra en el ejemplo siguiente.
Ejemplo
Represente en la recta numérica los siguientes números racionales:
  1. $\displaystyle \frac{3}{2}$
  1. $\displaystyle \frac{7}{2}$
  1. $\displaystyle \frac{-1}{2}$
  1. $\displaystyle \frac{-5}{2}$
Solución:
De igual manera, si se dividen en tres partes iguales cada segmento unidad en la recta, podemos representar los números racionales cuya representación fraccionaria tiene como denominador 3, como se muestra en el ejemplo siguiente.
Ejemplo
Represente en la recta numérica los siguientes números racionales:
  1. $\displaystyle \frac{4}{3}$
  1. $\displaystyle \frac{8}{3}$
  1. $\displaystyle \frac{-2}{3}$
  1. $\displaystyle \frac{-7}{3}$
Solución:
Generalizando el procedimiento descrito anteriormente se puede representar cualquier número racional en la recta numérica.
Ejercicio
Represente en un recta numérica los siguientes números racionales:
  1. $\displaystyle \frac{5}{2}$
  1. $\displaystyle \frac{7}{3}$
  1. $\displaystyle \frac{-9}{4}$
  1. $\displaystyle \frac{-14}{5}$
Solución
Nota: También se pueden representar los números racionales en la recta numérica, considerando su expansión decimal y ubicándolos en forma aproximada en la recta numérica, como se muestra en el ejemplo siguiente.
Ejemplo
Represente en una recta numérica los siguientes números racionales.
  1. $\displaystyle \frac{7}{9}$
  1. $\displaystyle \frac{34}{15}$
  1. $\displaystyle \frac{-9}{7}$
  1. $\displaystyle \frac{-17}{5}$
Solución
Utilizando la calculadora se puede notar que:
  1. $\displaystyle \frac{7}{9}=0,\overline{7}$
  2. $\displaystyle \frac{34}{15}=2,2\overline{6}$
  1. $\displaystyle \frac{-9}{7}=-1,\overline{285714}$
  2. $\displaystyle \frac{-17}{5}=-3,4$
De esta manera

Ejercicios
  1. Represente en una recta numérica los siguientes números racionales.

      1. $\displaystyle \frac{2}{3}$
      1. $\displaystyle \frac{8}{5}$
      1. $\displaystyle \frac{-5}{2}$
      1. $\displaystyle \frac{7}{4}$

      1. $\displaystyle \frac{9}{2}$
      1. $\displaystyle \frac{-11}{3}$
      1. $\displaystyle \frac{13}{5}$
      1. $\displaystyle \frac{-7}{4}$
  2. Utilice la calculadora para encontrar la expansión decimal de los siguientes números racionales y represéntelos en una recta numérica.

      1. $\displaystyle \frac{13}{7}$
      1. $\displaystyle \frac{7}{15}$
      1. $\displaystyle \frac{-65}{21}$
      1. $\displaystyle \frac{-85}{13}$

      1. $\displaystyle \frac{16}{9}$
      1. $\displaystyle \frac{77}{27}$
      1. $\displaystyle \frac{-40}{29}$
      1. $\displaystyle \frac{-134}{141}$




Solución





Un segmento comprendido entre dos números enteros consecutivos se llama segmento unidad.
Para representar el número racional $\displaystyle \frac{a}{b}$ en la recta numérica se divide cada segmento unidad en b partes iguales y se toman a de esas partes.

Para representar los números racionales en la recta numérica también se puede considerar su expansión decimal, de esta manera se ubican en la recta de manera 
Publicado por en No hay comentarios:
Suscribirse a: Entradas (Atom)